摘 要：接触电阻的计算与连接器热仿真的准确性密切相关，但目前还缺乏有效的方法。本文提出了一种基于粗糙表面接触电阻模型和有限元仿真的接触电阻和温升的精确获取方法，利用接触面轮廓和接触面基准面间距建立了接触电阻与接触温度的关系。我们采用三维热电耦合有限元仿真方法，建立了间隔距离和实际接触面积的等效接触电阻模型，以获取接触件温升数据，为接触电阻的计算和接触件温升的仿真提供了一种准确而有效的方法。

关键词：接触电阻模型;有限元仿真;接触电阻;接触件温升

1 引言

静态电接触在电气设备的接触和连接中极为常见。由于静态电接触在工作过程中不会产生电弧，因此最需要研究的问题是接触可靠性和热相关问题。接触电阻是产生热的主要来源，其计算与电接触热仿真的准确性密切相关。接触电阻的理论模型是对接触点尺寸、数量、分布规律以及材料性质、表面形貌和环境条件对接触电阻的影响的数学描述，一直是电接触领域人们关注的焦点。

不过，由于接触机理和影响因素的复杂性，接触电阻的数学模型进展较为缓慢。二十世纪三十年代，霍尔姆提出了电接触机理的基本理论，并基于一些理想的假设，给出了著名的单接触点接触电阻的霍尔姆模型。这一电阻模型没有考虑多点接触和表面膜层对接触电阻的影响^[1]。考虑到多点接触，格林伍德(Greenwood)和威廉姆森(Williamson)基于统计分析提出了一个粗略的接触模型，用于计算接触点的数量、实际接触面积和接触力 ^[2-5]。考虑到表面膜的影响，马鲁奇(Malucci)提供了接触电阻的三级约束模型，其中一些参数很难确定。格罗斯曼(Grosmann)总结了接触电阻随时间的变化规律，并根据丰富的实验数据提出了接触电阻的变化模型。R.W.卡文(R. W. Caven)还建立了两个接触面的接触电阻模型来预测接触电阻的分布。此外，这些电阻模型的还有一个缺陷就是没有考虑接触件温升问题，这就导致了仿真的复杂性和不确定性。

本文在粗糙曲面接触电阻模型的基础上，利用表面轮廓测量的参数建立了接触电阻模型。这些参数包括接触点数量、实际接触面积、接触力和接触表面的参照面之间的距离。此外，本文还利用实际接触电阻面积和间距建立了接触电阻的等效模型，并通过三维热电耦合有限元进行仿真，完成了接触件温升的计算和影响因素分析。本文的研究成果可为接触电阻和温升提供一个有效、准确的计算方法，为电接触的可靠性验证和优化电阻设计提供有益的参考。

2 粗糙表面接触模型

接触电阻表面并不是理想的光滑状态，而是粗糙不平的，如图1所示。当两个金属电阻表面接触时，氧化层被刮伤以形成导电路径(接触点)。两个粗糙金属表面的电接触是通过多个接触点来实现的，实际接触面积只是表观接触面积的一小部分，如图2所示。

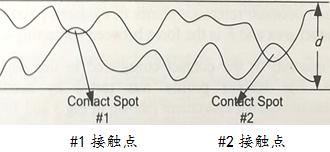
图1 粗糙表面示意图

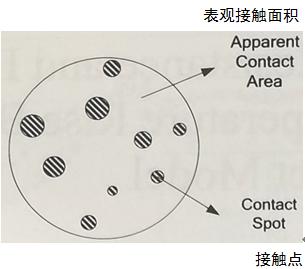
图2 实际接触面积示意图

粗糙面接触电阻模型将两个粗糙面之间的接触简化为刚性平面和等效可变形表面之间的接触，其假设条件如下：1)电阻接触点高度的分布类似于高斯分布;2)所有电阻接触点在顶点处具有相同的半径;3)电阻接触点高度变化具有随机性，并且电阻接触点单独出现变形。等效参数按照公式(1)来计算。

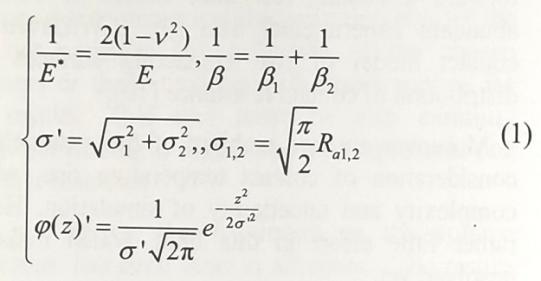
式中，E是弹性模量，E*是E的等效值，ν是泊松比，β_1，2接触点是两个电阻接触面的平均半径，β是接触点的等效平均半径，σ_1，2 RMS是电阻接触面的粗糙度，σ是等效RMS粗糙度，z是峰值高度之和，ψ(z)是高斯密度函数，ψ(z)'是具有等效参数的高斯密度函数，而R_a1,2是两个电阻接触表面的算术平均粗糙度。当接触件处于弹性变形状态时，粗糙表面接触电阻模型满足公式(2)中的要求。

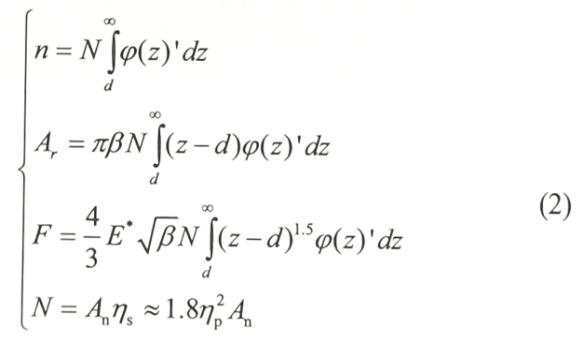
式中，n是电阻接触点数量，N是表观电阻接触区域峰值数量，A_n是表观接触面积，η_s(η_p)是平均面积(长度)上的峰值数量，d是电阻接触表面参照面之间的间隔距离，A_r是实际电阻接触面积，F是接触面之间的压力。

本文所研究的接触电阻材料为银氧化铬合金(AgCdO)。表面轮廓通过针型电阻粗糙度测量仪进行测试，见图3和表1。RMS粗糙度σ可通过公式(1)根据其粗糙度的算术平均值R_a进行计算。

图3 接触面侧面轮廓

表1 接触电阻表面粗糙度数据

电阻表面轮廓的测量还在取样长度L中提供了峰值高度数据。当z_i+1、z_i、z_i-1为相邻高度时，斜率m_i、曲率k_i、RMS斜率σ_m和RMS速曲率σ_k通过下列公式(3)来确定：

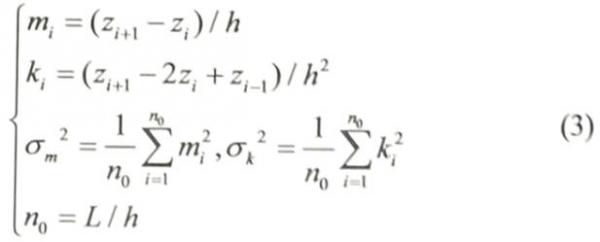
式中，n₀是取样数量，h是取样离散距离。

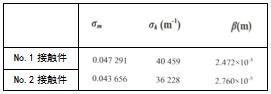
如果电阻接触点高度的分布类似于高斯分布，那么，平均曲率近似为σ_k的值。取样长度L为3.25x10^-3(m)，离散距离h为1.25x10^-3(m)。表2给出了电阻表面轮廓的统计分析结果。

表2 电阻表面轮廓数据的计算

为了计算电阻接触点的数量、接触力和接触面之间的实际电阻接触面积，现创建粗糙表面接触电阻模型公式(4)：

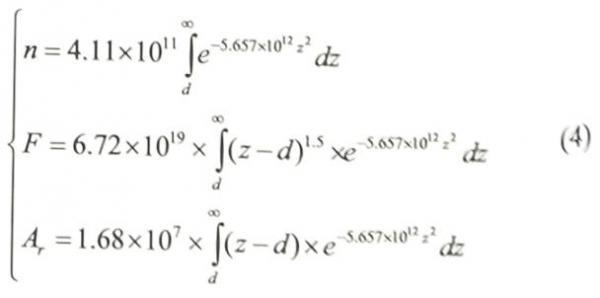
3 接触电阻模型

接触电阻R由收缩电阻R_c和膜层电阻R_f组成。收缩电阻R_c包括包络收缩电阻R₀和多点作用ρ/nd₀。其中，ρ是电阻率，d是触点平均直径。在接触件出现劣化，且电阻接触面存在氧化膜的情况下，应考虑到膜层电阻的作用。假设σ_f为通道电阻率，接触电阻模型可通过公式(5)来计算。

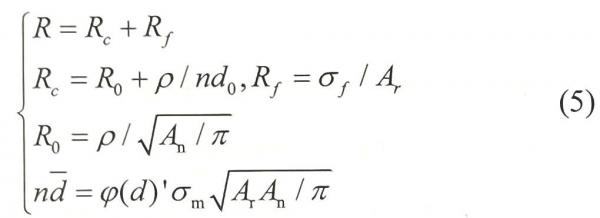
因此，我们可以根据接触力、实际接触面积和接触面基准面间距的计算结果建立接触电阻模型。ρ=2.8x10^-8(Ω·m)，其计算公式如下：

式中，系数C₁为5.6x10^-14，而C₃为1.4 x 10^-5，而C₂在本文中没有测定和使用。为了得到接触面接触电阻与接触力之间的关系式，本文在电阻距离限定在某一范围的条件下对其数据进行拟合。拟合表达式和曲线如公式(7)和图4所示。

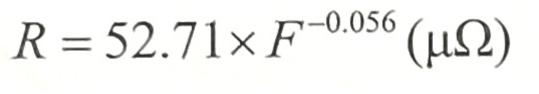 (7)

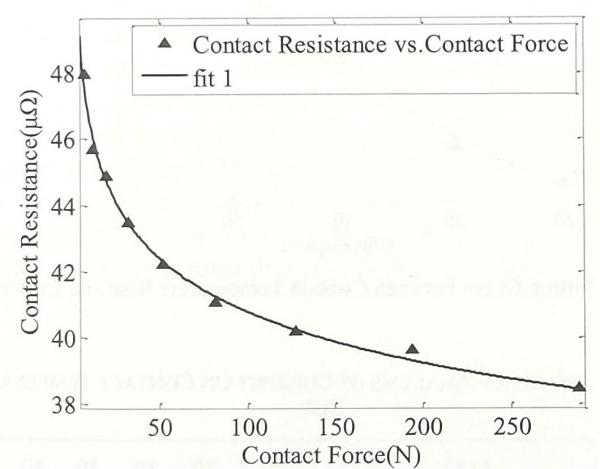
图4 接触电阻与接触力拟合曲线

文章还分析了电阻实际接触面积与接触力之间的关系，以供进一步研究，如图5所示。开始时，电阻实际接触面积随着接触力的增加而迅速增加，但在接触力增加到给定值之后，其增速明显放缓。

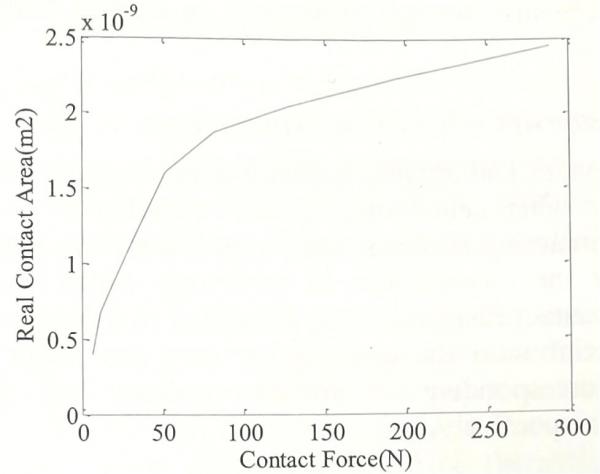
图5 电阻实际接触面积与接触力关系曲线

我们将本文获得的电阻模型和经验公式的接触电阻计算结果与不同接触力下的实验值进行对比，如表3所示。在工程应用中，常用的经验公式为R =k(0.102F)^-m。对于AgCdO平面接触件来说，式中的系数m为1，k为170。

表3 接触电阻结果对比

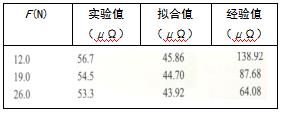
从拟合表达式获得的接触电阻小于从实验中获得的接触电阻。一方面，由于C₂的不确定性，该电阻模型没有考虑膜层电阻的影响，这可能是产生这种差异的主要原因;另一方面，曲率是一个假定的平均值也是产生差异的原因。从拟合表达式可以看出，接触电阻的变化规律与实验结果基本吻合。很明显，由于经验公式是基于一个粗略的视图得出的，因此其经验值与实验结果的差异更大。这种观点过分地考虑了接触力的影响，与实际情况并不相符。

通过对比可以看出，在某些情况下，由经验公式得到的接触电阻是不准确的，而本文提出的电阻模型更符合实验结果。

4 接触件温升仿真及其影响因素分析

接触件温升的分析非常复杂，因为它涉及到电流、接触力等许多影响因素，如接触材料的热和电气特性、环境条件、表面轮廓、接触尺寸等。本文所述的接触件温升仿真是基于根据公式(7)所计算的接触电阻。利用上述等效电阻模型，本节将进行三维热电耦合有限元仿真，进一步分析了电流、接触力和接触尺寸对接触件温升的影响规律。

4.1接触件温升仿真试验

本文在计算实际接触面积时已经考虑了多点接触的影响，为了便于建模，接触面之间的电接触可以视为一种单点接触。这意味着接触电阻模型可以简化为与接触件相同材料的圆柱体，圆柱体的面积和高度相当于实际接触面积及间隔距离。

接触电阻和接触件温升试验系统的有限元电阻模型如图6和图7所示。该测试系统由一对触点、等效接触电阻模型、夹具和其他一些金属零件组成。在接触力F为19(N)，电流I为60(A)，室温T₀为25℃的条件下，接触件温升的仿真结果如图8所示。

图6 接触电阻有限元仿真电阻模型

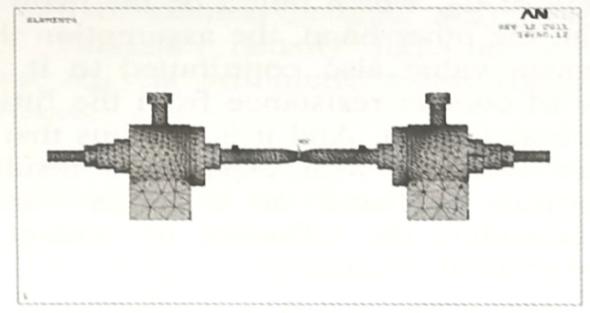
图7 接触件温升试验系统有限元仿真电阻模型

图8 接触件温升仿真结果

仿真试验中的接触件温升为76℃，而测得的温升值为85℃。接触件温升值差额就是由接触电阻差导致的，详见表3所示。

4.2接触力对温升的影响分析

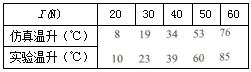
在I为60(A)和T₀为25℃条件下，接触件温升随接触力增大的变化规律如表4所示。

表4 压力对接触件温升的影响

仿真结果表明，接触件温升随着接触力的增大而减小，但其变化幅度逐渐变小。这恰好与上面分析的实际面积和接触力之间的影响规律完全吻合。

4.3电流对接触件温升的影响分析

我们分析了在F为19(N)，T₀为25℃的条件下，接触件温升随电流增加的变化规律。根据图9中所示的拟合曲线，其数据可根据公式(8)计算出来。

式中，△T是接触件温升仿真结果，I是电流。

图9 接触件温升与电流拟合曲线

表5 电流对接触件温升的影响分析

结果显示，接触件温升与电流的平方值成正比，而其系数(本文为0.021 14)与接触力、接触件热导率和电阻率有关。本文所介绍的方法提供了一种在指定接触材料和尺寸的情况下，在不同电流值下确定系数和计算接触件温升的方法。

4.4接触尺寸对接触件温升的影响分析

接触尺寸的变化会影响表观接触面积、触点数量和实际接触面积，从而改变接触电阻和接触件温升。在F为19(N)、I为60(A)和T₀为25℃的条件下，接触温度随触点半径R的增加而上升的变化情况如表6和图10所示。

表6 接触尺寸对接触件温升的影响分析

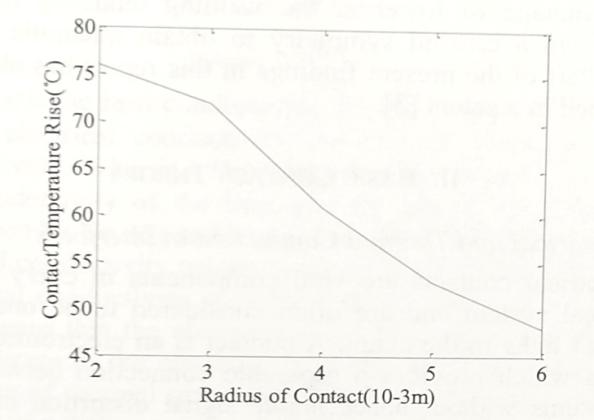
图10 接触件温升和触点半径之间的关系曲线

仿真结果表明，增大触点尺寸可以在一定范围内有效降低接触件温升。在接触半径增加到一定数值后，这种影响会有所减弱，因为在一定范围内，表观接触面积对实际接触面积的增加作用很小。因此，在接触结构的优化设计中，需要进行理论计算和仿真分析，以确定适宜的触点尺寸。

5 结论

1)本文提出了一种基于粗糙表面接触电阻模型，通过表面轮廓测量和统计分析计算出平面接触电阻的方法。文中还得到了接触电阻与接触力的拟合关系。这项研究通过实验得到了验证。

2)提出了用接触电阻模型仿真接触件温升的方法。在此基础上，通过三维热-电耦合有限元仿真计算出接触件温升，分析了接触力、电流和接触尺寸对接触件温升的影响。

3)本文的研究成果为接触电阻的计算和接触件温升的仿真提供了一种准确而有效的方法，可应用于不同材料的接触件，也为电接触的可靠性验证和优化设计提供了很好的参考。

参考文献：

[1] Holm R. Electrical Contacts. New York: Springer, 1979.

[2] Greenwood J.A., Williamson J.B.P. Contact of Nominally Flat Surfaces. Proc. of the Royal Society, 1966, A295: 300-319.

[3] Greenwood J.A. Constriction Resistance and the Real Area of Contact. Brit. Appl. Phys., 1966,17: 1621-1632

[4] Greenwood J.A. The Area of Contact between Rough Surfaces and Flats. Journal of Lubrication Technology,1967,p81-87.

[5] Greenwood J.A, Tripp JH. The Contact of Two Nominally Flat Rough Surfaces. Proc. Instn. Mech.,1970-71,Engrs185: 625-633.