摘 要：采用有限元分析法(FEA)为带有一排针孔连接器的PCB组件在双波焊接工艺中的热感应翘曲建模，将PCB板的热翘曲估算值与试验所得到的测量值进行比较。结果发现，该模型可以示出在焊接过程中以及在焊接之后的组件变形。通过对具有不同PCB和连接器材料特性的影响参数进行研究，可以得出这些特性选择的一般性原则。

关键词：针孔连接器;PCB组件;热膨胀;翘曲

1 引言

印制电路板(PCB)的热机械分析一直是各种元件性能分析和数值研究的主题，例如采用一种有限元模型方法对PCB板各层热膨胀系数失配影响进行研究。为此，我们建立了针孔组件中连接器插针热感应变形和镀孔周围的应力模型，并进行相关分析。目前，人们为未插合连接器以及配有表面安装元件的PCB板热翘曲建立了相应的模型。

本研究旨在开发一种可以预测PCB组件(PCBA)的热机械特性。这种PCB组件由3个主要元件组成：一排带有磷青铜插针的热塑性针孔(PTH)连接器、由替代层铜薄片和FR-4玻璃纤维/环氧树脂复合层组成的PCB板以及焊接的针孔连接头。在制造过程中，将安装在PCB板上的针孔连接器组件熔融、预热，并以一个较小的仰角通过熔融焊剂一个补充的驻波进行传送。PCB组件的热转移与波的接触面积、温度和转移速度成正比。由于加热作用的不均匀性，PCB组件的几何形状及组件中各个元件热机械特性的不同，PCB组件中产生一定的残存应变，并可能导致在插针连接中产生过大的翘曲和应力。

本文的目的旨在利用有限元分析法(FEA)对PCB组件在波焊过程中的热机械特性建立一种模型，并对作为各种PCB和连接器材料特性函数的总体PCB组件翘曲进行相关研究。

2 有限元模型

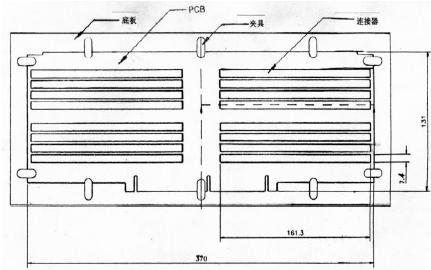
所有模型的建立和分析均采用运行于Silicone Graphics Challenge L工作站的ANSYS 5.3有限元软件来完成。该组件的几何形状为沿着PCB平面的两轴(见图1(a))对称分布，因此只需要将实际组件的1/4部分建立模型即可。在波焊过程中，印制电路板沿着边缘在几个点位夹持于一块钛铝合金托板上(见图1(a))，连接器垂直方向的翘曲变形也得到有效的抑制。实际组件上的翘曲测定显示它只出现在x-y平面上(见图1(b))。这是由于其外形的对称性以及工艺加热的均匀特性所决定的。因此，PCB组件的变形可以采用穿过其中一个连接器的二维剖面来建立相关的模型，参见图1(a)和图1(b)。

(a)

(b)

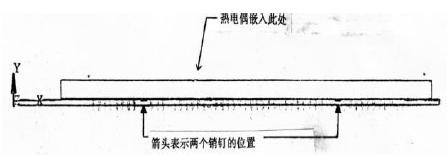
图1(a)PCBA平面图显示焊接过程中连接器的布局和所用夹具的位置;垂直于中心线的虚线表示可由模型表示的部分;(b)表示图1(a)中虚线的剖面图以及夹具和热电偶位置

因此，有限元模型由通过一排50插针(实际连接器有200个插针，分4排排列，每排50个插针)与连接器相连接的PCB组成。PCB模型长为185mm，厚度为1.57mm，其针孔直径为0.81mm，而连接器模型长为161.3mm，厚度为5.8mm，插针的截面积为0.41mm×3mm。将连接器定位在PCB板上(实际上，这些连接片位于连接器插针的中间两排)的两个塑料连接片，参见图1(b)。

图1(b)的几何外形采用二维、8个节点、平面应力和四边形结构元的ANSYS 5.3进行离散分析。其网格由1443个元和5549个节点组成，参见图1(a)和图1(b)。它代表4种材料：印制电路板、连接器、插针和焊料。

PCB和连接器(图2(a))在整个波焊过程中的临界温度曲线采用与一个数据记录器相连接的热电偶来测定。将两个热电偶放置于连接器中(嵌入连接器的上端和下端)，另外3个热电偶嵌入PCB板中(上端、中心部位和下端)。PCB板中的温度变化梯度可以忽略不计(见图3(a))，而连接器中的温度则在上、下端之间呈现出线性变化规律。由图2(a)可以看出，在波焊过程中的某一给定时间，连接器和PCB的温度是不同的。尤其是，PCB的温度开始下降后，连接器的温度却继续上升。此外，我们还观察到，如果PCB在进行波焊处理时没有加装连接器的话，就会出现零翘曲现象。这一点也值得注意。

图2(a)图1(b)中所示意的模型的有限元网格，(b)网格详图显示单孔、焊料接和插针(1-连接器;2-插针;3-PCB;4-焊料)

这一模型分4个步骤完成，分别对应于实际波焊过程中的4个阶段，即预热和熔融焊料的施加、冷却使焊料固化、从焊机排出后即进行冷却以及拆除夹具。所测得的温度(图3(a))确定每个步骤(图3(b))所采用的温度，将从一个步骤到下一个步骤的温度变化作为一条线性上升线建立其相关模型。

我们可以假定该组件在室内温度下(20℃)不存在任何残存应力。利用x-方向的对称性(图1(a))将波焊4个步骤中的零水平位移(x方向)强加于模型的左端。在步骤1~3中，连接器应固定于PCB板两个塑料连接片的位置(图1(b))。在步骤1~3中，夹具夹持着PCB组件，并约束PCB底面和连接器上端，使之只沿着水平方向(x方向)移动，参见图3(a)和图1(b)。在第4步骤中，拆去夹具，只保留右下端的节点使其只沿着水平方向(x方向)移动，而其垂直方向(y方向)的运动则受到约束。这就使得模型的左端相对于受约束的右下角发生最终纵向变形。

有限元分析法的第一步就是PCB组件的预热和焊剂的添加，使之填充于PCB孔和连接器插针之间的空间。在这一步骤中，可以用“死的”单元(其刚度可忽略不计)来表示熔融的焊料，使得插针可以在PCB孔内产生不受约束的相对运动。

有限元分析法的第二步就是PCB板的冷却和焊机中的焊料开始固化，但连接器温度仍在上升，见图3(a)。开始固化时，这些“死的”单元被激活(在3个“负载步骤”中指定了一个有限刚度)。在随后的步骤(3和4)中，这一刚度逐渐增大，以便将随着温度的降低而出现的焊料的模量增大建立一个模型(在3个步骤中，每个步骤其刚度均上升到一个新的值)。

第三步是将来自波焊焊机的PCBA出口、连接器和PCB的冷却过程建立一个相关模型。

第四步是从夹具上拆除PCBA(电路板和连接器的垂直(y)约束)，并最终冷却至室内温度。

3 材料特性

表1列出PCB、连接器和该模型中所用插针的特性。PCB和连接器的热膨胀系数(CTE)采用一个TMA2940热机械分析仪来测得，而其他所有特性则来自有关文献，或由制造厂家提供。这些特性可以视为与温度(即低于有关聚合物的玻璃临界温度的某一合理的近似值)无关。在这一工艺过程中，实际温度只是在一个较短的时间内超过PCB板的玻璃临界温度(T_g=158℃)，见图3(a)。此外，我们还可以从该模型中看出，约70%的翘曲变形发生在最后的冷却阶段，其温度大大低于PCB板的玻璃临界温度。温度较低时，其机械特性对温度的依赖性较弱。

表1 PCB和插针热机械特性以及连接器特性参数

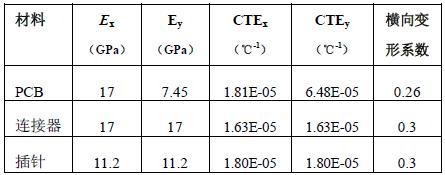
PCB可以看作一种线性弹性材料，在x和y方向具有不同的杨氏弹性模量值。连接器和插针可以作为匀质和线性弹性材料来建立相关模型。其线性弹性特性在有关电路板特性模型中经常使用，并在下列两个因素分析研究中进一步加以阐明：PCB板在一个较短的时间内超过其玻璃临界温度(T_g=158℃)(参见图3(a));设计本模型旨在预测球状翘曲和目前尚未具体说明的应力状态。

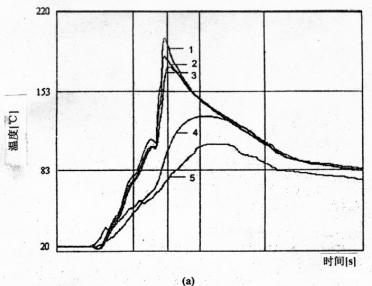
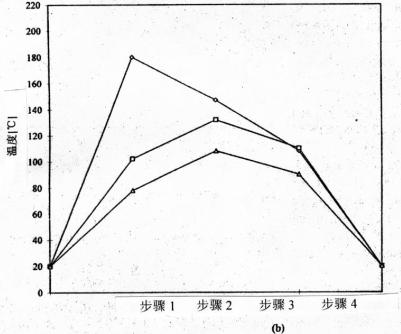
图3(a)波焊过程中的热电偶读数;(b)该模型4个步骤所采用的温度

焊料(含有63%重量锡和37%重量铅)的热机械特性见表2所列，并给出作为温度函数的杨氏(弹性)模量。

4 结果与讨论

图4表示双波峰焊接工艺后半个PCB组件预计的最终变形形状。将预计的PCB组件最大翘曲与测得的最大翘曲(标准IPC-TM-650中方法2.4.22)进行对比，其相对差值小于5%。此外，还对同一块PCB板上的其他两种连接器材料的翘曲测量值进行比较，结果发现：1)当E=17Gpa，CTE=2.8×10^-5 ℃^-1时，测得的最大翘曲与预计的最大翘曲之间的相对差值为8%;2)当E=17Gpa，CTE= 0.5×10^-5℃^-1时，测得的最大翘曲与预计的最大翘曲之间的相对差值为6%。

图4 发生最终变形的PCB组件，可以看出受应力变形程度最高的插针

通过对PCB组件每个元件的Von Mises应力进行相关检测后发现，焊料一般都是应力最高的材料。特别是，邻近两个连接器连接片(图1(b))的焊接点出现了最大的Von Mises应力。不过，需要指出的是，本模型的主要目的还是测算PCB板翘曲的总体应力。要准确预测焊接点的最大应力要求一个更为精细的网格，在可能情况下还需要提供更具体的与温度有关的焊料机械特性以及PCB和连接器的非线性特性。

连接器通常置于图1(a)中所示的位置。每个连接器板内末端与中心线的距离约为24mm。为了测算出连接器定位的翘曲敏感度，应采用板内末端与中心线的距离约为4mm的连接器模型。这就将预计的最大翘曲度由原来的2.8mm增至3.4mm。

从某种程度来说，PCB组件翘曲是PCB板、连接器和焊料热机械特性的变化函数，也是温度和波焊工艺引发的温度梯度的变化函数。为了更好地理解热机械特性对翘曲的相对影响，我们分别改变PCB板和连接器的杨氏弹性模量(E_x)和热膨胀系数(CTE)，而PCB组件的其他特性则保持在正常值水平，见表1和表2。为了便于比较PCB板对翘曲所产生的相对作用，应按照下列公式(1)确定其敏感度参数：

S = |(Δω/ω)/(Δb/b)|               (1)

式中，ω为标称翘曲(用表1和表2中的特性来获得相应的翘曲值)，b为标称特性值(见表1和表2)，Δω为翘曲的变化量，而Δb则为特性值变化量。由此可见，绝对敏感度是其特殊特性对最大翘曲产生相对作用的一种反映。例如，当S=1时，特殊特性变化10%，PCB板最大翘曲就会相应地发生10%的变化。

表2 作为步骤1、2和4中所用温度函数的焊接特性

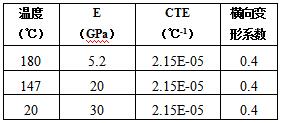
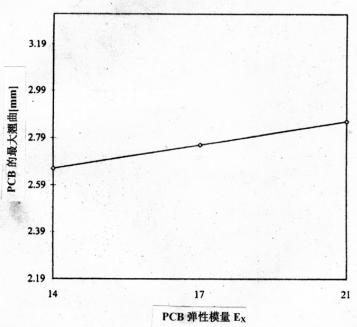
图5最大翘曲与连接器E_x关系曲线

图6 最大翘曲与连接器E关系曲线

通过图5可以看出，其最大翘曲随着PCB的E_x增大而有所增大，其敏感度为S=0.2。连接器的E发生变化会产生相反的作用(参见图6)，虽然其对这一特性的敏感度更高，即S=0.3。最大翘曲对PCB板和连接器的热膨胀系数CTE的变化更为敏感，分别参见图7和图8。在x方向增大PCB的热膨胀系数CTE(约为标称值)，翘曲就会随之增加(见图7)，其S=1.2。相比之下，连接器热膨胀系数CTE增大(约为标称值)，其翘曲度则会随之减小(见图8)，其S =0.73。

图7最大翘曲与x方向的PCB板CTE关系曲线

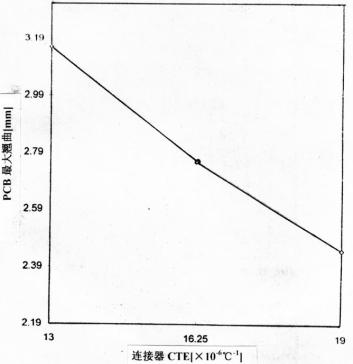
图8 最大翘曲与连接器CTE关系曲线

值得注意的是，连接器特性的变化通常要比PCB特性变化更容易获得，因为PCB是一种层叠式铜薄片。尽管如此，一般可能很难做到不降低杨氏弹性模量(E)并增大翘曲(见图6)来大幅度地增大连接器的热膨胀系数(并因此减小其翘曲度，见图8)，虽然由于热膨胀系数CTE的变化，后一种作用大大小于前一种。

前面所述的敏感性分析考虑到较小的PCB和连接器特性变化(约为标称值的20%)。重点关注作为使用寿命最长的连接器，以考虑其特性变化。该模型应在更大的连接器CTE值范围内运行，以确定PCB组件的翘曲是否能够消除，至少理论上如此。将所有其他模型参数保持于标称值，见表1和表2。可以发现，当连接器的CTE值约为40×10^-6℃^-1时，其翘曲度为零。超出这一值，PCB组件将沿着图4所示的相反方向发生翘曲，即在连接器下面出现凹面。

上述讨论涉及到建立一个模拟实际工艺过程的模型。这样一来，在夹持点将PCB组件紧紧夹住，使之在y方向不会发生任何翘曲变形。为了测算模型4个步骤中各个步骤所产生的最终翘曲有多大，应拆去夹具，进行几个循环的测试。可以看出，约70%的最终翘曲发生在第4个步骤，而30%发生在第1~3步骤中。

5 结论

采用有限元模型方法可以提供带有一排对称PTH连接器的PCB在波焊之后的总体热翘曲精确预测值。从各种热机械特性作用的参数研究可以看出，PCB热翘曲对PCB和连接器的热膨胀系数(CTE)的变化最为敏感;同时，我们还发现连接器的热膨胀系数(CTE)增大2.5(其他特性参数不变)的情况下，可以消除其热翘曲现象，且整个翘曲中的约70%预计发生在最后冷却阶段。

参考文献：

[1] W.Bolton, Engineering Materials Handbook. Boca Raton, FL: CRC, 1989.

[2] P van Dijk, Å.Kassman Rudolphi and D.Klaffke: Investigations on Electrical Contacts Subjected to Fretting Motion, Proc ICEC Conf., 2002.

[3] Pendleton W.E., Tackett A., Korzeniowski L., Cvijanovich G.B., Williams R.T., Jones W.C. : Computer Simulation of Topographical Changes on Gold Contact Surfaces Caused by Loading, , Proc. Holm Conf., 1998, pp. 120-126.